Maass wave form
In mathematics, a Maass wave form is a function on the upper half plane that transforms like a modular form but need not be holomorphic. They were first studied by Maass (1949).
Definition
A Maass wave form is defined to be a continuous complex-valued function f of τ = x + iy in the upper half plane satisfying the following conditions:
- f is invariant under the action of the group SL2(Z) on the upper half plane.
- f is an eigenvector of the Laplacian operator
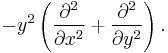
- f is of at most polynomial growth at cusps of SL2(Z).
A weak Maass wave form is defined similarly but without the growth condition at cusps.
See also
References
- Bump, Daniel (1997), Automorphic forms and representations, Cambridge Studies in Advanced Mathematics, 55, Cambridge University Press, ISBN 978-0-521-55098-7, MR1431508
- Maass, Hans (1949), "Über eine neue Art von nichtanalytischen automorphen Funktionen und die Bestimmung Dirichletscher Reihen durch Funktionalgleichungen", Mathematische Annalen 121: 141–183, doi:10.1007/BF01329622, MR0031519